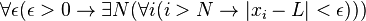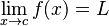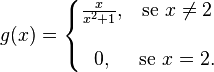Amai-vos uns aos outros como eu vos amei...

Limites

23-07-2013 13:24

Em matemática, o conceito de limite é usado para descrever o comportamento de uma função à medida que o seu argumento se aproxima de um determinado valor, assim como o comportamento de uma sequência de números reais, à medida que o índice (da sequência) vai crescendo, i.e. tende para infinito. Os limites são usados no cálculo diferencial e em outros ramos da análise matemática para definir derivadas e a continuidade de funções.

Índice

[esconder]

Limite de uma sequência[editar]

Ver artigo principal: Limite de uma sequência

Seja $x_1, x_2, \ldots$ uma sequência de números reais. A expressão:

$\lim x_i = L$

significa que, quanto maior o valor i, mais próximo de L serão os termos da sequência. Neste caso, dizemos que o limite da sequência é L.

A forma usual de escrever isso, em termos matemáticos, deve ser interpretada como um desafio. O desafiante propõe quão perto de L os termos da sequência devem chegar, e o desafiado deve mostrar que, a partir de um certo valor de i, os termos realmente estão perto de L.

Ou seja, qualquer que seja o intervalo em torno de L (dado, pelo desafiante, por exemplo, pelo intervalo aberto $(L - \epsilon, L + \epsilon) \mbox{ , em que } \epsilon > 0$ , o desafiado deve exibir um número natural N tal que $\forall i (i > N \rightarrow x_i \in (L - \epsilon, L + \epsilon))$ .

Formalmente, o que foi dito acima se expressa assim:

$\forall \epsilon (\epsilon > 0 \rightarrow \exists N (\forall i (i > N \rightarrow |x_i - L| < \epsilon)))$

Limite de uma função[editar]

Ver artigo principal: Limite de uma função

Suponhamos que f(x) é uma função real e que c é um número real. A expressão:

$\lim_{x \to c}f(x) = L$

significa que f(x) se aproxima tanto de L quanto quisermos, quando se toma x suficientemente próximo de c. Quando tal acontece dizemos que "o limite de f(x), à medida que x se aproxima de c, é L". Note-se que esta afirmação pode ser verdadeira mesmo quando 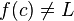$f(c) \neq L$ , ou quando a função f(x) nem sequer está definida em c. Vejamos dois exemplos que ajudam a ilustrar estes dois pontos importantíssimos.

Consideremos 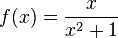$f(x) = \frac{x}{x^2 + 1}$ à medida que x se aproxima de 2. Neste caso, f(x) está definido em 2 e é igual ao seu limite: 0.4, vejamos:

f(1.9)	f(1.99)	f(1.999)	f(2)	f(2.001)	f(2.01)	f(2.1)
0.4121	0.4012	0.4001	$\Rightarrow$ 0.4 $\Leftarrow$	0.3998	0.3988	0.3882

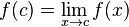À medida que x aproxima-se de 2, f(x) aproxima-se de 0.4 e consequentemente temos a igualdade $\lim_{x\to 2}f(x)=0.4$ . Sempre que se verifique a igualdade $f(c) = \lim_{x\to c} f(x)$ , diz-se que fé contínua em x = c. A igualdade não é válida para todas as funções. Vejamos uma função onde tal não acontece

$g(x)=\left\{\begin{matrix} \frac{x}{x^2+1}, & \mbox{se }x\ne 2 \\ \\ 0, & \mbox{se }x=2. \end{matrix}\right.$

O limite de g(x) à medida que x se aproxima de 2 é 0.4 (tal como em f(x)), mas 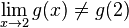$\lim_{x\to 2}g(x)\neq g(2)$ e consequentemente g não é contínua em x = 2.

Consideremos agora o caso onde f(x) não está definida em x = c.

$f(x) = \frac{x - 1}{\sqrt{x} - 1}$

Apesar de f(x) não estar definida em x = 1, o limite de f(x), quando x se aproxima de 1, existe e é igual a 2:1

f(0.9)	f(0.99)	f(0.999)	f(1.0)	f(1.001)	f(1.01)	f(1.1)
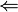1.95	1.99	1.999	$\Rightarrow$ não está definido $\Leftarrow$	2.001	2.010	2.10

Ora x pode ser tomado tão próximo de 1 quanto quisermos, sem no entanto ser 1, pelo que o limite de $f(x)$ é 2.2

Definição formal[editar]

A definição ε-δ de limite.

O conceito de limite é formalmente definido da seguinte forma: Seja $f$ uma função definida num intervalo aberto $I$ contendo $a$ (excepto possivelmente $a$ ) e seja $L$ um número real. A expressão

$\lim_{x \to a}f(x) = L$

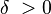significa que qualquer que seja $\varepsilon\ >0$ existe um $\delta\ >0$ tal que para todo 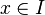$x \in I$ , satisfazendo $0<|x-a|< \delta$ , vale $| f (x)-L|< \varepsilon$ . OU, usando a notação simbólica:

$\lim_{x \to a} f(x) = L \Leftrightarrow \forall \epsilon > 0, \exists \delta > 0 : \left ( x \in I\;\wedge 0 < | x - a | < \delta \right ) \Longrightarrow | f(x) - L | < \epsilon$

Dito de maneira mais formal, um limite L é dado da seguinte maneira, segundo a ideia originalmente formulada por Cauchy:

um limite L dado pela fórmula:

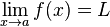
$\lim_{x \to a}f(x) = L$

onde L é o valor do qual difere o valor de $f$ a menos de um valor ε (epsilon) maior que zero se o valor de x diferir de a por um valor menor que o valor δ (delta) maior que zero e função de ε (δ = f(ε))

$\delta = g(\epsilon) > 0 \Rightarrow 0 <|x-a|<\delta \to |f(x)- L| < \epsilon$

Aproximação intuitiva[editar]

A noção de limite é fundamental no início do estudo de cálculo diferencial. O conceito de limite pode ser aprendido de forma intuitiva, pelo menos parcialmente.

Quando falamos do processo limite, falamos de uma incógnita que "tende" a ser um determinado número, ou seja, no limite, esta incógnita nunca vai ser o número, mas vai se aproximar muito, de tal maneira que não se consiga estabelecer uma distância que vai separar o número da incógnita. Em poucas palavras, um limite é um número para o qual y = f(x) difere arbitrariamentemuito pouco quando o valor de x difere de x0 arbitrariamente muito pouco também.

Por exemplo, imaginemos a função: $f(x)=2x+1$ e imaginando $f:R->R$ (Definida nos reais). Sabemos, lógico, que esta função nos dá o gráfico de uma reta, que não passa pela origem, pois se substituirmos: $f(0)=2.0+1$ que nos dá: $f(0)=0+1 = 1$ , ou seja, no ponto onde x=0 (origem), o y (f(x)) é diferente de zero. Mas usando valores que se aproximem de 1, por exemplo:

Se x=0,98 então: y=f(x)=2,96
Se x=0,998 então: y=f(x)=2,996
Se x=0,9998 então: y=f(x)=2,9996
Se x=0,99999 então: y=f(x)=2,99998

Ou seja, à medida que x "tende" a ser 1, o y "tende" a ser 3. Então no processo limite, quando tende a ser um número, esta variável aproxima-se tanto do número, de tal forma que podemos escrever como no seguinte exemplo:

Exemplo 1.1: Sendo uma função f definida por: $f(x)=2x+1$ nos Reais, calcular o limite da função $f$ quando $x -> 1$ . Temos então, neste caso, a função descrita no enunciado e queremos saber o limite desta função quando o "x" tende a ser 1: Ou seja, para a resolução fazemos:

Então, no limite é como se pudéssemos substituir o valor de x para resolvermos o problema. Na verdade, não estamos substituindo o valor, porque para o cálculo não importa o que acontece no ponto x, mas sim o que acontece em torno deste ponto. Por isso, quando falamos que um número "tende" a ser n, por exemplo, o número nunca vai ser n, mas se aproxima muito do número n. Enfim, como foi dito anteriormente, a definição de limite é tão e somente intuitiva. Vai de analisar a função que está ocorrendo apenas. Agora, o exercício do Exemplo 1.1 mostra que x se aproxima de 1 pela esquerda, ou seja:

Porém, temos também uma outra forma de se aproximar do número 3, na função $f(x)$ descrita nos exemplo acima, por exemplo: Se x=2, y=f(x)=5 ; Se x=1,8 então: y=f(x)=4,6 ; Se x=1,2 temos que: y=f(x)=3,4 ; Se x=1,111 então: y=f(x)=3,222 Podemos perceber então, que x está tendendo a 1 pela direita agora, e não mais pela esquerda como foi mostrado no exemplo anterior. Então para resolvermos problemas que envolvem cálculo, devemos saber como a função que está em jogo se comporta.

Limites em funções de duas ou mais variáveis[editar]

A noção de limite, conquanto seja a mesma para todos os tipos de funções numéricas, nem sempre é fácil de se calcular. Muitas vezes é mesmo difícil de se afirmar que o limite exista ou não. A função distância entre os objectos da função, na definição formal anteriormente apresentada para uma variável, dada por $| x - a |$ , não pode ser utilizada. Neste contexto, surge a necessidade de uma função distância. Nesse caso, a definição de limite é a seguinte3 :

Seja $f$ uma função do tipo:

$D \subseteq \mathbb{R}^n \rightarrow \mathbb{R}$ $x \longmapsto f(x) = z$

Em que $x$ é um vector com $n$ coordenadas e $z$ um número real. Se $a$ for um vector com $n$ coordenadas, então:

$\lim_{x \to a} f(x) = L \Leftrightarrow \forall \epsilon > 0, \exists \delta > 0 : \left ( x \in D\;\wedge 0 < d(x,a) < \delta \right ) \Longrightarrow | f(x) - L| < \epsilon$

Em que $d(x,a) = \| x - a \|$ é a função distância.

Exemplo[editar]

Uma função do tipo:

$\mathbb{R}^2 \rightarrow \mathbb{R}$ $(x,y) \longmapsto f(x,y) = z$

pode ter evidentemente um limite, mas aqui há uma diferença fundamental.

Sobre a reta real, só existe verdadeiramente um grau de liberdade, ou seja, só se pode ir para a direita (no sentido de maiores números reais) ou para a esquerda (no sentido de menores números reais).

Com uma função de duas variáveis (só para ficar no caso mais simples) tem-se dois graus de liberdade. Consequentemente, pode-se ter infinitos caminhos entre dois pontos, o que na verdade influencia o valor do limite.

Ora, para que exista um valor de limite, é necessário que ele seja independente do caminho tomado para que o(s) valor(es) da(s) variável(eis) independentes sejam alcançados. Isso é verdade no caso unidimensional, quando os dois limites laterais coincidem. Caso contrário, o limite não existe.

De forma semelhante, quando se tem uma função bidimensional como:

$\mathbb{R}^2 \rightarrow \mathbb{R}$ $(x,y) \longmapsto f(x,y) = xy$

o limite pode ser testado através de vários caminhos.

Suponha que se queira verificar o seguinte limite L desta funçao:

$\lim_{(x,y) \to (0,0)}f(x,y)) = L$

Pode-se aproximar-se do valor (0,0) através das seguintes possibilidades (de entre uma infinidade delas):

o limite através do eixo dos $yy$ , ou seja,

$\lim_{x \to 0}f(x,0) = L$

Nesse caso o limite L é zero.

o limite através do eixo dos $xx$ , ou seja,

$\lim_{y \to 0}f(0,y) = L$

Nesse caso, o limite L é também zero.

Poder-se-ia ficar enumerando todas as possibilidades, mas seria ocioso. No caso dessa função, o limite nesse ponto é sempre zero, conforme demonstraremos.

Vamos, então, provar que

$\lim_{(x,y) \to (0, 0)} xy = 0$

Ou seja, provar que

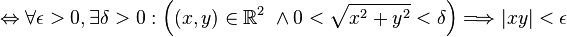
$\forall \epsilon > 0, \exists \delta > 0 : \left ( (x,y) \in \mathbb{R}^2\;\wedge 0 < \| (x,y) - (0,0) \| < \delta \right ) \Longrightarrow | xy - 0| < \epsilon$ $\Leftrightarrow \forall \epsilon > 0, \exists \delta > 0 : \left ( (x,y) \in \mathbb{R}^2\;\wedge 0 < \sqrt{x^2 + y^2} < \delta \right ) \Longrightarrow | xy | < \epsilon$

Vamos procurar escrever $\delta$ em função de $\epsilon$ .

$\sqrt{x^2 + y^2} < \delta \Leftrightarrow x^2 + y^2 < \delta^2$ (I)

$|xy| \leq \max\{|x|,|y|\}^2 \leq x^2 + y^2 < \delta^2$ (II), usando (I)

Se escolhermos $\delta = \sqrt{\epsilon}$ , então, por (II), $|xy| < \delta^2 = \epsilon$ , o que prova o nosso limite.

Um exemplo de uma função que não apresenta valor de limite em (0,0) é a função:

$\mathbb{R}^2 \rightarrow \mathbb{R}$ $(x,y) \longmapsto f(x,y) = {xy \over (x^2+y^2)}$

que pode ser provado fazendo-se a aproximação do ponto (0,0) através das parametrizações dadas pelas equações paramétricas:

$x = \left(\cos \alpha\right)t$

$y = \left(\sin \alpha\right)t$

a função toma a forma

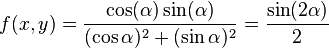
$f(x,y) = {\cos(\alpha)\sin(\alpha) \over (\cos\alpha)^2+(\sin\alpha)^2} = {\sin(2\alpha) \over 2}$

Vê-se, então, que o valor do limite depende do ângulo α pelo qual a reta de parametrização permite que se aproxime do ponto (0,0). Dessa forma, o limite não existe nesse ponto para essa função.

[Esconder] v • e Funções
Tipos	Analítica • Bijetora • Convexa • Divisor • Elementar • Exponencial • Fatorial • Identidade • Inclusão • Inteira • Inversa • Iterada • Limitada • Logaritmo • Logaritmo natural •Monótona • Parcial • Polinomial • Retangular • Simples • Sinal • Sobrejetora • Suave
Trigonométricas	Cosseno • Seno • Tangente • Cotangente • Cossecante • Secante
Hiperbólicas	Cosseno hiperbólico • Cossecante hiperbólica • Seno hiperbólico • Secante hiperbólica • Tangente hiperbólica
Famosas	Ackermann • Bessel • Dirichlet • Gama • Heaviside • Mertens • Möbius • Weierstrass
Conceitos	Assimptota/Assíntota • Curva • Derivada • Espaço funcional • Espaço Lp • Gráficos • Integral • Limite • Injectividade • Parte inteira • Primitiva • Projeção • Reta
Funções em Economia	Demanda • Oferta • Utilidade

Voltar

Contacto

ARR UM POUCO DE PAZ E ESPITIRO Angola, Brasil, Estados Unidos, Portugal, França, Alemanha, Rússia, Espanha e Inglaterra. ricardorep3g@hiphopfan.com ricardorep3g@hotmail.com +244936804363

Questionário

Gostou deste Site

Muito Bom (106)

Bom (14)

Bom, mais podia ser melhor (27)

Não gosto (19)

Tenta dar mais um retoque que vai ser algo mais que bom (21)

Total de votos: 187

Calendário de Eventos

11 de Novembro de 1975 em Angola

09-11-2010 15:28

Cerimonia da Independência de Angola - 11 de Novembro de 1975 A independência de Angola foi proclamada por António Agostinho Neto, primeiro Presidente da República Popular de Angola e do MPLA. Foi às 23:00 horas do dia 11 de Novembro de 1975 que Agostinho Neto proclamava...